Variance

We’ve seen that mean, median, and mode are used to find the central tendency of the data distribution. In other words, they help us to summarise the central values of the data. But centres can be the same for different datasets too. In those cases, we use the measure of dispersion to describe the data. Variance is one such measure of dispersion.

For example, consider these two lists.

[-300, -200, -100, -100, 0, 100, 100, 200, 300]

[-3, -2, -1, -1, 0, 1, 1, 2, 3]

Now if you were to find the mean and median for both the lists, it will be the same. Zero! Let’s visualise that quickly with Python.

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt


# Data
sierra_points = np.array([-300, -200, -100, -100, 0, 100, 100, 200, 300])
tango_points = np.array([-3, -2, -1, -1, 0, 1, 1, 2, 3])

# Mean
print("Mean of sierra is: {}.".format(np.mean(sierra_points)))
print("Mean of tango is: {}.".format(np.mean(tango_points)))

# Median
print("Median of sierra is: {}.".format(np.median(sierra_points)))
print("Median of tango is: {}.".format(np.median(tango_points)))

# Plot
plt.subplot(121)
plt.title("Sierra")
plt.xlabel("Points")
plt.ylabel("Counts")
plt.xlim(-300, 700)
plt.ylim(0, 5)
plt.hist(sierra_points)
plt.axvline(np.mean(sierra_points), color='g', linestyle='dashed', linewidth=1)

plt.subplot(122)
plt.title("Tango")
plt.xlabel("Points")
plt.ylabel("Counts")
plt.xlim(-50, 50)
plt.ylim(0, 5)
plt.hist(tango_points)
plt.axvline(np.mean(tango_points), color='g', linestyle='dashed', linewidth=1)

plt.show()

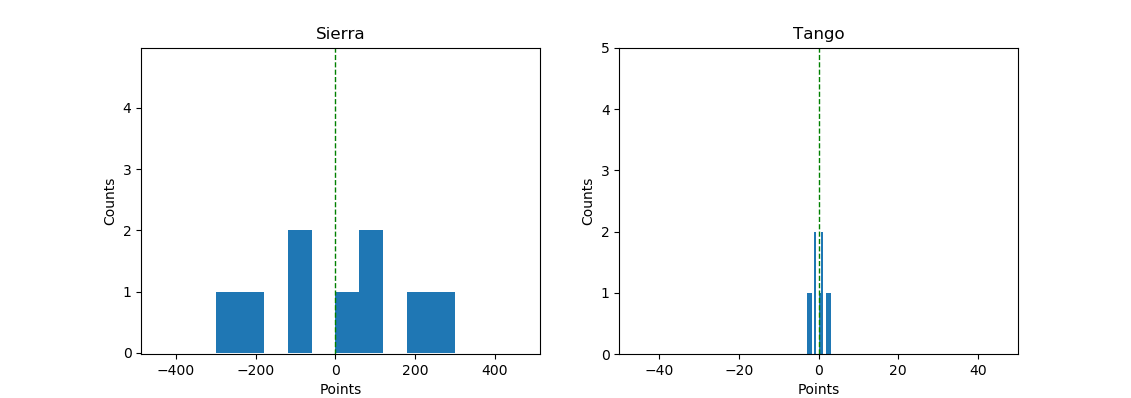
So, in this case, the measure of central tendency is worthless when you have to compare two different datasets. But look at how different the ‘spread’ is for these two data between -300 to 300. The first list is pretty stretched all the way from -300 to 300. The second list is tightly packed around -3 to 3. This measure of ‘how far the data is spread out or scattered across’ is called variance.

If we calculate the distance between the mean and each of the data points, we could get an idea of how scattered these data points are. Once we get the differences, the variance of the whole dataset is just the average of all the differences (squared to prevent negative numbers).

Mathematically, variance $\sigma^{2}$ can be expressed as follows.

$$\sigma^{2}=\frac{\sum_{i=1}^{N}\left(X_{i}-\mu\right)^{2}}{N}$$

Where $X-\mu$ is the difference between the data point $X$ and mean $\mu$, and $N$ is the total number of differences.

To calculate the variance with numpy modify the above code and add np.var(sierra_points) and np.var(tango_points). You’d find the variance of each list to be 33333.3 and 3.3 respectively.